This post originated from Lab 1 of course Compilers: Principles that I’m currently taking, in which we were required to write a flex program to parse a subset of the C language. The multiline comment /* */ was the most troublesome to handle for most of us (excluding me, for sure).
The process
I’ll assume you’ve already drawn a DFA for the multiline-comment structure, so here it is:
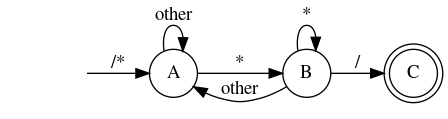
We’re first going to turn it into “state transformation equations”, so it looks like this:
\[A = \texttt{/*} \mid A\texttt{[^*]} \mid B\texttt{[^*/]} \\ B = A\texttt{*} \mid B\texttt{*} \\ C = B\texttt{/}\]The first step we’re taking is to realize that $A=S \mid Aa$ is easily found to be equivalent to $A = Sa^*$, where the superscript asterisk means “repeat 0 or more times”. So $B$ can be turned into
\[B = A\texttt{**}^* = A\texttt{*}^+\]Again, the superscript plus means “repeat 1 or more times” as the same in PCRE.
Now it’s time to substitute $B$ with its simplified expression:
\[A = \texttt{/*} \mid A\texttt{[^*]} \mid A\texttt{*}^+\texttt{[^*/]} \\ C = A\texttt{*}^+\texttt{/}\]Note that there’s a distributive property here, which described using symbols, is that $Aa \mid Ab = A(a\mid b)$, so now we have
\[A = \texttt{/*} \mid A\ (\texttt{[^*]} \mid \texttt{*}^+\texttt{[^*/]})\]Applying the first transformation $A = S \mid Aa = Sa^*$, we have
\[A = \texttt{/*}\ (\texttt{[^*]} \mid \texttt{*}^+\texttt{[^*/]})^*\]Now there’s no recursion in the new “state transformation equation”, so we can substitute $A$ with this final expression and get the regular expression for $C$, the result we want:
\[C = A\texttt{*}^+\texttt{/} = \texttt{/*}\ (\texttt{[^*]} \mid \texttt{*}^+\texttt{[^*/]})^*\ \texttt{*}^+\texttt{/}\]Converting the above regular expression to code, we now have
C = \/\*([^*]|\*+[^*/])*\*+\/
Try it online with RegEx101!
Now can you imagine how to use regular expressions to match multiples of 3 (base 10)? Yes, it’s entirely possible. See this fantastic article for details, which uses essentially the same techniques to convert a DFA (or a finite-state machine) to a regular expression that does the job.



Leave a comment