题目(P248 例 3)
设弦的一端($x=0$)固定,另一端($x=l$)以 $\sin\omega t \; \color{red}{(\omega\ne\frac{n\pi a}l,\;n=1,2,\ldots)}$ 作周期振动,且初值为零,试研究弦的自由振动。
问题:研究当 $\omega \to \frac{n\pi a}l,\;n=1,2,\ldots$ 的时候的弦的振动。
解答
要想研究这个特殊情况的振动,首先要观察原问题的求解过程。
1. 原问题的求解过程
依题意,得定解问题
\[\left\{ \begin{align} \cfrac{\partial^2u}{\partial t^2} = a^2 \cfrac{\partial^2u}{\partial x^2} \; (0<x<l, t>0) \tag{3}\label{eq3} \\ u(t,0) = 0, \, u(t,l) =\sin\omega t \tag{4}\label{eq4} \\ u(0,x)=0, \, u_t(0,x) = 0 \end{align} \right.\]由于边界条件是非齐次的,首先应把边界条件齐次化。选取合适的 $v(t,x)$ 使得 $v$ 既满足泛定方程,又满足边界条件,这时再令 $u=v+w$ 后得到的关于 $w(t,x)$ 的泛定方程也是齐次的。
为此,令
\[v(t,x)=X(x)\sin\omega t\]由边界条件 $\eqref{eq4}$,可知 $X(0)=0,X(l)=1$。把 $v(t,x)$ 代入泛定方程 $\eqref{eq3}$,且消去 $\sin\omega t$,得
\[X''+\cfrac{\omega^2}{a^2}X=0\]所以
\[X(x)=C_1\cos\cfrac{\omega x}a+C_2\sin\cfrac{\omega x}a\]由 $X(0)=0$ 得 $C_1=0$;再由 $X(l)=1$,得
\[C_2=\cfrac 1{\color{red}{\sin\cfrac{\omega l}a}}\]从而可得
\[X(x) = \cfrac 1{\sin \cfrac{\omega l}a}\sin\cfrac{\omega x}a \\ v(t,x) = \cfrac {\sin\cfrac{\omega x}a}{\sin \cfrac{\omega l}a}\sin\omega t\]将 $v(t,x)$ 的表达式和 $u=v+w$ 代回原定解问题,就得到关于 $w$ 的定解问题
\[\left\{ \begin{array}l \cfrac{\partial^2w}{\partial t^2} = a^2 \cfrac{\partial^2w}{\partial x^2} \; (0<x<l, t>0) \\ w(t,0) = w(t,l) = 0 \\ w(0,x)=0, \, w_t(0,x) = -\omega\cfrac{\sin\cfrac{\omega x}a}{\sin\cfrac{\omega l}a} \end{array} \right.\]由公式解得
\[w(t,x) = 2\omega al\sum_{n=1}^{+\infty}\cfrac{(-1)^{n+1}}{\color{red}{(\omega l)^2-(n\pi a)^2}}\sin\cfrac{n\pi at}l\sin\cfrac{n\pi x}l\]相加可得
\[u(t,x) = \cfrac {\sin\cfrac{\omega x}a}{\color{red}{\sin \cfrac{\omega l}a}}\sin\omega t + \\ 2\omega al\sum_{n=1}^{+\infty}\cfrac{(-1)^{n+1}}{\color{red}{(\omega l)^2-(n\pi a)^2}}\sin\cfrac{n\pi at}l\sin\cfrac{n\pi x}l\]
这就是原问题的解。
2. 解的分析
从上面的原问题的解可以很直观的发现一点:当 $\omega\to\cfrac{n\pi l}a$ 的时候,会有 $\sin\cfrac{\omega l}a \to \sin n\pi=0$ 以及 $\omega l=n\pi a$ 的情况,进而导致多个地方出现分母为 $0$ 的现象。这些部分已用红色标出。也就是说
\[\lim_{\omega \to \frac{n\pi l}a}u(t,x)=\infty ,\, n=1,2,\ldots\]求解一个定解问题,一般包含三个步骤。上面的过程就算是完成了第一个步骤——分析步骤,即从数学和物理的角度出发,找出了所要的解。
接下来的步骤与书上相同,跳过第二个步骤——综合步骤,即论证所求得的解的确是原问题的解,满足泛定方程和定解条件的步骤——直接进入第三个步骤,对所求得的解进行物理解释。
3. 对所求得的解进行物理解释
对于我们当前求得的这个含有无穷值的解,对其直接进行物理解释并不容易,因此需要从头再看看整个问题的结构。
3.1 问题的提出
本问题 “理想弦的横振动方程” 在书上的 P197 提出。这里我们忽略提出过程中大量的简化过程,直接观察结果 (P199)
\[\cfrac{\partial^2u}{\partial t^2} = a^2 \cfrac{\partial^2u}{\partial x^2} + f(t,x) \\ \left( a = \sqrt{\cfrac T\rho} ,\, f(t,x)=\cfrac{g(t,x)}\rho \right)\]由于本问题讨论的是弦的自由振动,因此 $f(t,x)=0$,所以问题化为
\[\cfrac{\partial^2u}{\partial t^2} = a^2 \cfrac{\partial^2u}{\partial x^2} ,\; \left( a = \sqrt{\cfrac T\rho} \right)\]考虑到本问题的特殊条件 $\omega = \cfrac {n\pi a}l$,因此这里需要讨论一下 $a$ 的物理意义($l$ 是弦长,这无需讨论)。为了简化讨论过程,这里先忽略问题的定解条件,专注于泛定方程的物理意义。
3.2 一维波动方程中参数 $a$ 的物理意义
设一根张力为 $T$,密度 $\cfrac{\mathrm{d}m}{\mathrm{d}l}=\rho$ 的理想弦作自由振动,取其在惯性参考系下的一个波峰附近的一个微元,如图
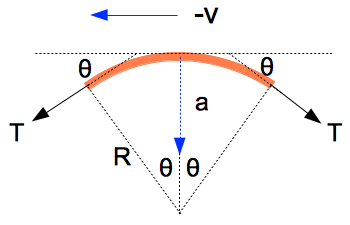
设这一小段弦的曲率半径为 $R$,则该段微元对应的加速度
\[a_\bot = -\cfrac{v^2}{R}\]其沿竖直方向所受的合力
\[F_\bot = -2T\sin\theta \approx -2T\theta\]又因为
\[l=2R\theta\]得
\[F_\bot = -2T\theta = \rho \cdot 2R\theta\left(-\cfrac {v^2}{R}\right) \\ \therefore v = \sqrt{\cfrac T\rho}\]这时候我们发现,弦上的波速 $v$ 就是一维波动方程的参数 $a$。但是这有什么意义呢?
3.3 驻波与固有频率
回想力学中学过的驻波相关的内容,两列传播方向相反,而振幅、频率都相同的波相遇时,会形成驻波。由于驻波的两端均固定,因此其波长 $\lambda$ 满足
\[2l=n\lambda ,\, n=1,2,\ldots\]而波的频率
\[f=\cfrac v\lambda=\cfrac{nv}{2l} ,\, n=1,2,\ldots\]则波的角频率
\[\omega = 2\pi f = \cfrac{n\pi v}l\]从上一节中我们得到了波速 $v$ 与方程参数 $a$ 的一致性,因此这里用 $a$ 替代 $v$ 后可得
\[\color{red}{\omega = \cfrac{n\pi a}l} \color{black}{,\, n=1,2,\cdots}\]也就是说,$\omega = \cfrac{n\pi a}l$ 是长度为 $l$ 的弦作自由振动的固有频率!当 $n=1$ 时,称 $\omega_1 = \cfrac{\pi a}l$ 为基频,同时也可以知道,一根弦的固有频率一定是基频的整数倍。
3.4 共振
谈到固有频率,就不得不讨论共振。在一个机械系统中,当受迫振动的频率与结构的固有频率相吻合,就会有共振的发生。在共振频中,受迫振动只需要很小的驱动力,就可在系统中产生巨大的振幅。
结合以上分析过程,我们判断,当 $\omega \to \cfrac{n\pi a}l$ 时,在 $u| _ {x=l}$ 端产生的胁迫振动的频率将在弦上产生共振,进而导致振幅随时间的推移可以无限增大,这与理论计算中出现的 $\lim _ {\omega \to \frac{n\pi l}a}u=\infty$ 相符。
而共振在历史上非常有名的一次出现,是塔科马海峡吊桥 (Tacoma Narrows Bridge) (1940 年版)。1940 年塔科马海峡吊桥建成通车后不到 5 个月就倒塌了,而倒塌的原因,是因为其桥面厚度不足,在受到强风的吹袭下引起卡门涡街,使桥身摆动;当卡门涡街的振动频率和吊桥自身的固有频率相同时,引起吊桥剧烈共振,最终因振幅过大而崩塌。
4. 计算机模拟
为了使问题的求解过程更容易理解,我使用了计算机软件 Wolfram Mathematica 12.0 进行绘图模拟。
4.1 准备工作
首先将 $u(t,x)$ 的解导入软件,定义为函数:
u[t_, x_] :=
2*a*l*\[Omega]*
Sum[
((-1)^(n + 1)*Sin[(Pi*n*x)/l]*Sin[(Pi*a*n*t)/l])/((l*\[Omega])^2 - (Pi*a*n)^2),
{n, 1, 20}
] + (Sin[t*\[Omega]]*Sin[(x*\[Omega])/a])/Sin[(l*\[Omega])/a]
这里由于计算机计算方式的限制,无法将 $\sum_{n=1}^{+\infty}$ 导入计算。经过测试,当累加上限为 $20$ 时,该函数已经能够提供很好的近似结果了,因此出于各种考虑(尤其是计算资源的利用),这里就取累加上限为 $20$ 了,因此实际绘图的函数是:
\[u(t,x) = \cfrac {\sin\cfrac{\omega x}a}{\sin \cfrac{\omega l}a}\sin\omega t + 2\omega al\sum_{n=1}^{20}\cfrac{(-1)^{n+1}}{(\omega l)^2-(n\pi a)^2}\sin\cfrac{n\pi at}l\sin\cfrac{n\pi x}l\]接下来为函数选定合适的参数。根据上面的分析结果,$a$ 为波的传播速率,为了产生较为明显的观察效果,经过测试,我决定选取 $l=10$ 与 $a=1$,则基频 $\omega = \cfrac{\pi a}l = \cfrac \pi{10}$。
确定好了参数,就可以开始绘图了。
4.2 静态 3D 绘图
如图,当 $\omega = 0.5$ 时,$\omega$ 与任意固有频率都有足够的偏差,此时得到的波形较为随机:
l = 10; a = 1; \[Omega] = 0.5;
Plot3D[u[t, x], {x, 0, 10}, {t, 0, 50}]
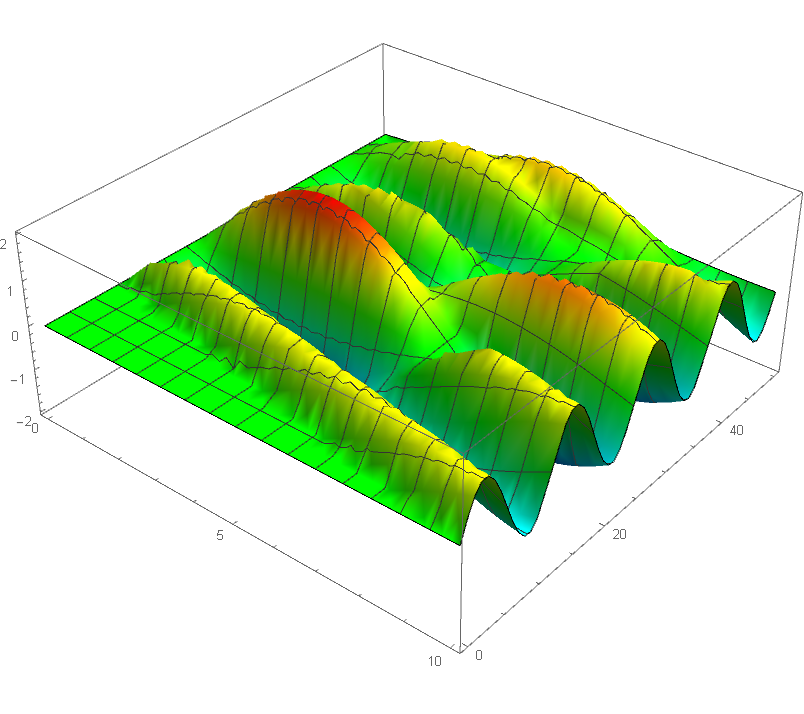
当 $\omega$ 接近基频 (即 $n=1$) 时,可以看出发生了共振现象,振幅随时间不断增大。这里考虑到计算机不能处理分母为零的情况,因此参数 $\omega$ 不能取基频 $\cfrac\pi{10}$,而必须与该值有微小差别,因此我取了 $0.31$。
l = 10; a = 1; \[Omega] = 0.31;
Plot3D[u[t, x], {x, 0, 10}, {t, 0, 200}]
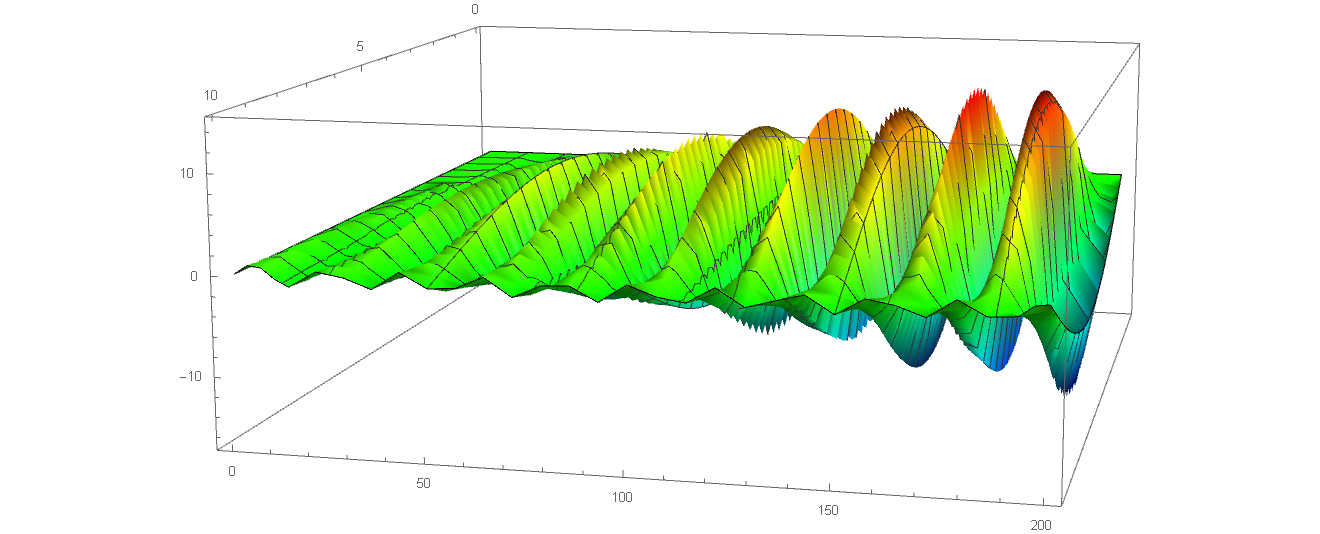
而当 $\omega$ 接近基频的某个整数倍时,同样能观察到共振现象,但驻波的数量不是一个,而是 $n$ 个。下图取 $n=3$ 绘制:
l = 10; a = 1; \[Omega] = 3*Pi/10 + 1/1000;
Plot3D[u[t, x], {x, 0, 10}, {t, 0, 60}]
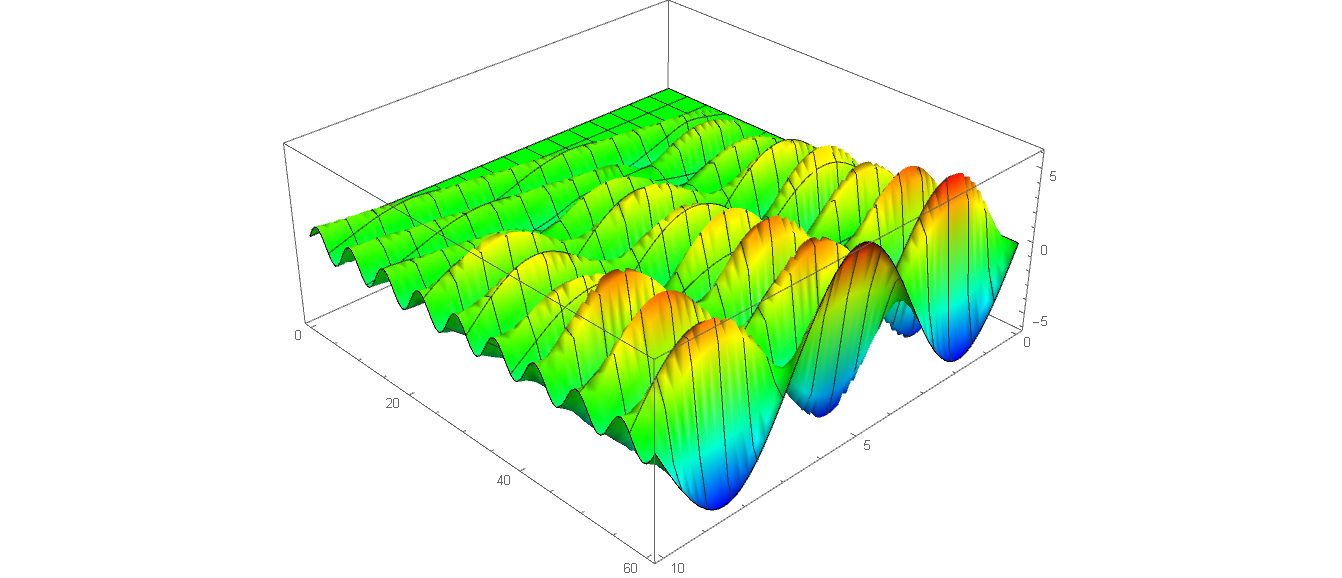
4.3 动态图像
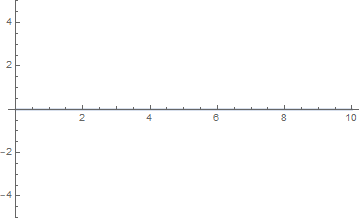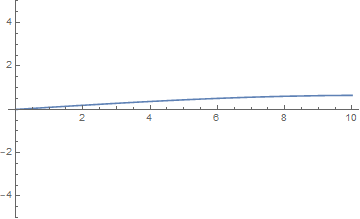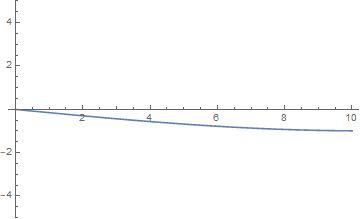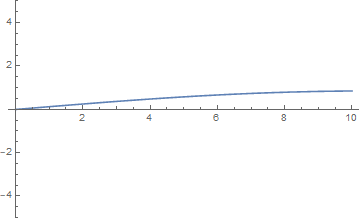
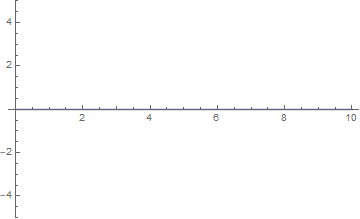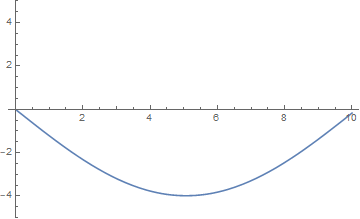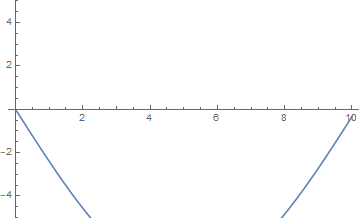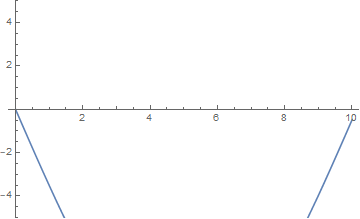
通过将一维波形用动态图像展示出来可以很直观地看出不同的 $\omega = \cfrac {n\pi a}l$ 对弦的自由振动的影响。以下几张图分别取 $n=\cfrac 12,1,2,4$ 绘制。
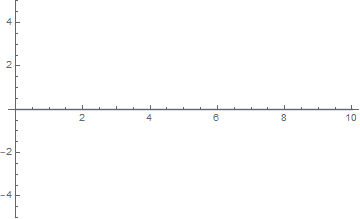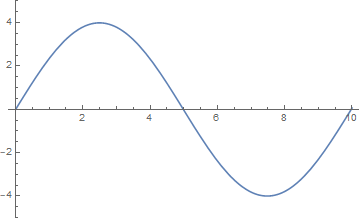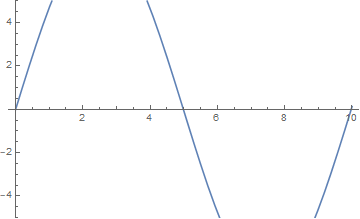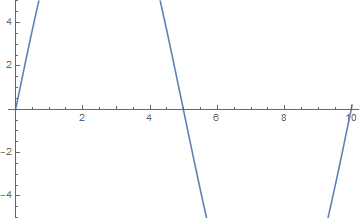
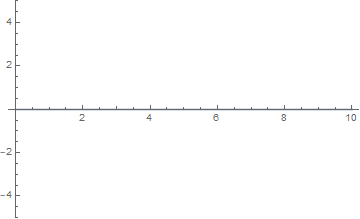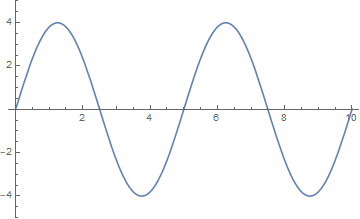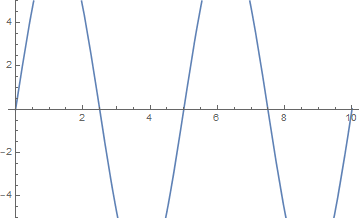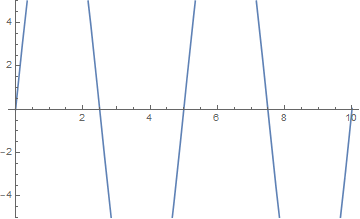
当 $n = \cfrac 12$ 时,右端的受迫振动看起来与弦并不和谐,振幅维持在 $1$ 以下:
l = 10; a = 1; \[Omega] = 0.15;
Animate[
Plot[u[t, x], {x, 0, 10}, PlotRange -> {-5, 5}], {t, 0, 300},
AnimationRate -> 30]
当 $n=1$ 时,右端受迫振动与弦的基频相吻合,弦的自由振动的振幅随右端受迫振动的影响而不断增大:
l = 10; a = 1; \[Omega] = 0.31;
Animate[
Plot[u[t, x], {x, 0, 10}, PlotRange -> {-5, 5}], {t, 0, 120, 0.4},
AnimationRate -> 30]
而当 $n$ 取大于 $1$ 的整数时,受迫振动的频率与弦的某个非基固有频率相吻合,结果是出现了多个驻波,且它们的振幅仍然不断增大:
l = 10; a = 1; \[Omega] = 0.63;
Animate[
Plot[u[t, x], {x, 0, 10}, PlotRange -> {-5, 5}], {t, 0, 120, 0.4},
AnimationRate -> 30]
l = 10; a = 1; \[Omega] = 1.257;
Animate[
Plot[u[t, x], {x, 0, 10}, PlotRange -> {-5, 5}], {t, 0, 120, 0.4},
AnimationRate -> 30]
以上就是我对 $\omega \to \frac{n\pi a}l,\;n=1,2,\ldots$ 的时候的理想弦的自由振动的非齐次混合问题的研究。
Leave a comment